Ternary Computing: Advantages and Future Potential
Ternary Computing: Advantages and Future Potential
Can Ternary Computing Improve Information Assurance?
The base 3, or ternary, system offers several advantages over the binary system, which is the standard for most computing today. Here are some key benefits:
1. Numerical Efficiency
Ternary systems are more efficient in terms of the number of digits required to represent large numbers. For example, a number that requires 42 bits in binary would need only 27 trits in ternary. This efficiency is measured by the radix economy, which is the product of the base and the number of digits needed to represent a number. Ternary has a lower radix economy than any other integer base for large numbers.
2. Reduced Query Complexity
Ternary logic can answer questions with more than two possible outcomes in a single query. For instance, when comparing two numbers, a ternary system can determine if one is less than, equal to, or greater than the other in one step, whereas a binary system would require multiple queries.
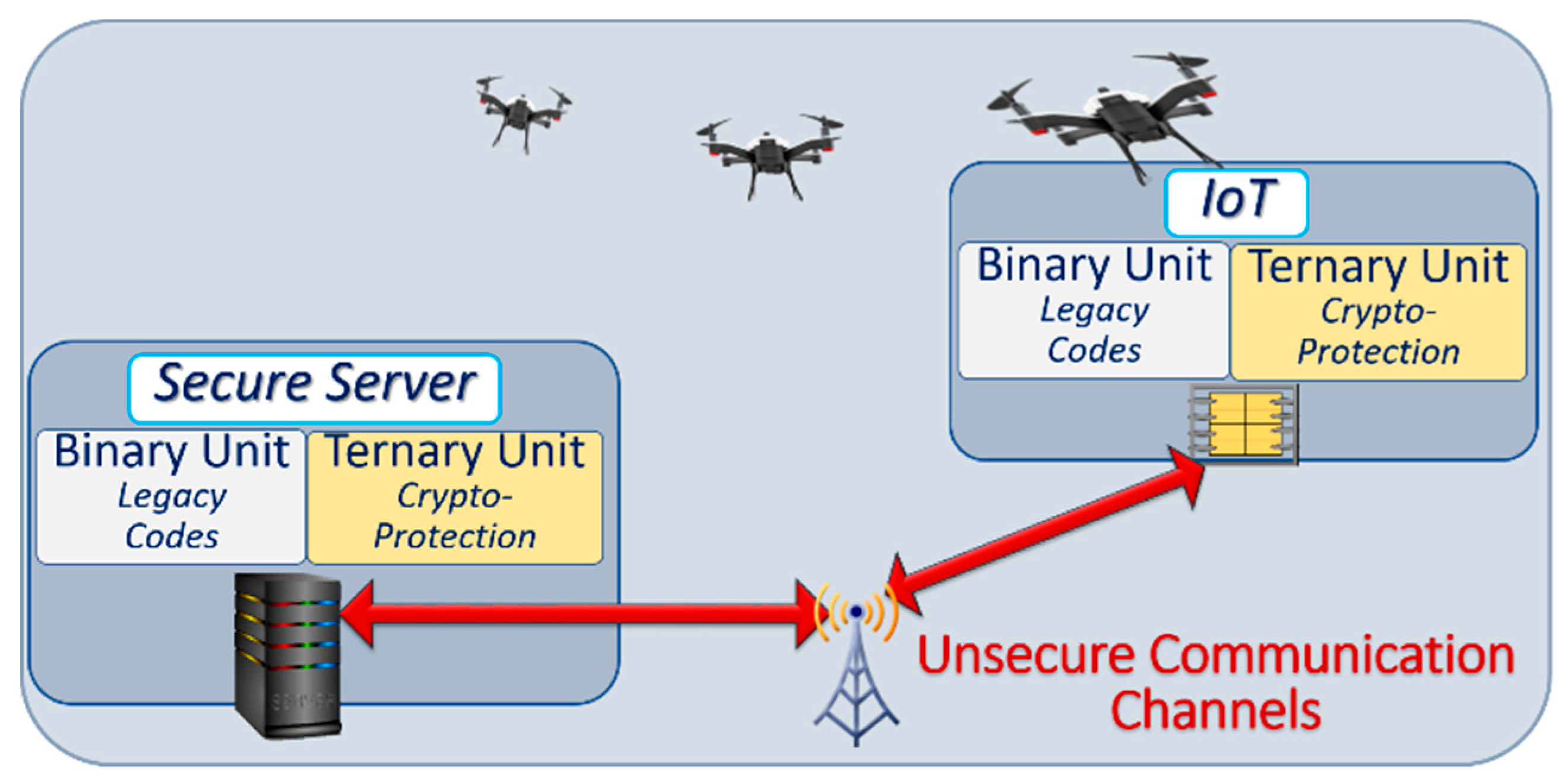
3. Better Error Management
Ternary states can better manage erratic information, leading to a reduction in error rates. This is particularly useful in cybersecurity applications, where managing and verifying data integrity is crucial.
4. Historical and Modern Developments
While ternary computing has been explored since the 19th century, it has seen recent advancements. For example, Soviet scientists developed the Setun computer in the 1950s, and modern researchers are proposing ways to integrate ternary logic into existing binary hardware.
5. Potential for Advanced Applications
Ternary computing can be applied to various advanced fields, such as cybersecurity, where it can improve the efficiency and reliability of public key infrastructure. Additionally, ternary systems can be used to optimize data compression and other computational tasks.
Despite these advantages, the adoption of ternary computing has been limited by the established binary infrastructure and the ease of implementing binary systems. However, ongoing research and development suggest that ternary computing may yet find significant applications in the future.
Invite Gmail Contacts
